単なるクイズ大会ではありません。
脳力頂上決戦は単なるクイズ大会ではありません。学ぶことの楽しさ、新しい知識を得る喜び、仲間と切磋琢磨する充実感を味わうためのイベントです。
現代の学習環境では、テストや成績に追われることが多いですが、本当に大切なのは知識を得る過程で培われる探究心や好奇心です。本大会では、難問に挑戦することで、自分の限界に挑む楽しさを体験していただけます。また、仲間との交流を通じて、共に学び合うことの素晴らしさを実感できます。本大会を通じて、学ぶことの楽しさを再発見し、仲間との絆を深めていただけることを願っています。
決勝戦は12/13(土)!!横浜本社ビルにて開催。
決勝戦の優勝チームには優勝賞品を授与いたします。
詳細
| 対象学年 | 中1・中2 ※臨海セミナーにお通いでない方もご参加いただけます。 |
|---|---|
| 会場・日時 | 予選：神奈川県内の教室で実施 会場により日時が異なります。詳細は下記のpdfをご参照ください。 中1の会場はこちら※ |
| 出題範囲 | 英語・数学・国語・理科・社会・特色・雑学などから出題されます。 |
| ルール |
|
―― 参加者一人ひとりのエントリーが必要です。――
お通いでない方のエントリーには保護者様によるご入力をお願いしております。
類題に挑戦！
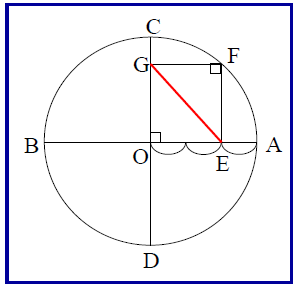
半径10cmの円Oにおいて、線分AB,CDはOの直径であり、AB⊥CDである。
線分OA上にOE:EA=2:1となる点Eをとり、Eを通りOAに垂直な線と弧ACとの交点をFとする。
また、FからOCに向かって下ろした垂線とOCとの交点をGとする。
このとき、線分EGの長さを求めなさい。
解答はこちら
【解答】 10cm
【解説】
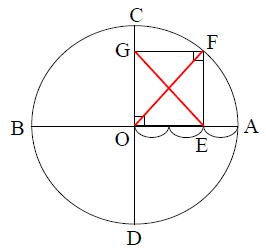
四角形OEFGは長方形なのでEG=OF
OFは円Oの半径なのでOF=10cm
よってEG=10cm
前回参加者の声
- 全て難しい問題だったけど、ためになるものも多かったから楽しかったです。
- 同じ学校の友達や塾の友達と仲を深めるきっかけとなりました。
- もう一度挑戦したいです！
- 問題は難しかったけれど、友達と協力して考えられたので勉強になりました。
- 正解できた時の喜びは大きかったです。
- 頭を使うような問題が多かったので楽しかったです。
