授業料・実績・面倒見で全国No.1の地域貢献を目指します。
タウンニュースの問題、みんな解けたかな?
中学校で配布されたタウンニュースに載っている臨海セミナーの広告、見てくれましたか?
アンケートの問題の答え、みんなはわかったかな?

正解はこちら!!

ベン図(集合を円の形で整理した図)を書いて考えましょう(図1)。
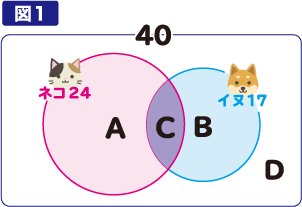
40人のクラスの中に、「ネコがいる人:24 人」の円と「イヌがいる人」の円があります。
「イヌがいる人」は、「いない人」が23人ですので、
40-23=17(人)です。
Aは「ネコだけがいる人」、Bは「イヌだけがいる人」です。
2つの円が重なっているC の部分は、「ネコがいて、かつ、イヌもいる人」を表します。
Dは「ネコがおらず、かつ、イヌもいない人」です。
「ネコだけがいる人は、イヌだけがいる人の2倍」ですので、これは
A=2B・・・① の関係になっている事を表しています。
次に「家に黒ネコがいる人」を考えます。
「黒ネコ」は全てが「ネコ」の中に含まれますので、(図2)のように表せます。
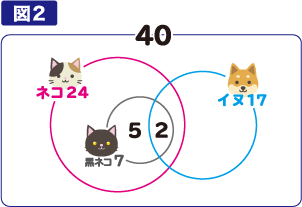
「家に黒ネコがいる人:7 人」で、「そのうちイヌもいる人:2人」ですから、「黒ネコがいて、かつイヌはいない人」は
7-2=5(人)となります。
ここで、この問題で求めたい「黒ネコ以外のネコがいて、かつ、イヌはいない人」を「x」と置く事にします。
つまり(図3)のE の場所がx人です。
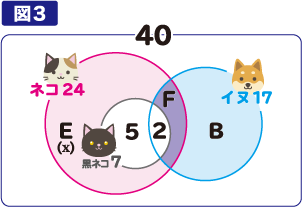
ここから、「ネコだけがいる人(図1のA)」は、
A=x+5・・・② と考えることができます。
さらに、(図3)のFは、ネコがいる人からxと、黒ネコがいる7人を引けば良いので
F=24-x-7=17-x と表せる事が分かります。
最後に、「イヌだけがいる人」であるB は、イヌがいる人から黒ネコがいる2人とFを引いて、
B=17-2-(17-x)=x-2 ・・・③となります。
したがって①~③より、x+5=2(x-2)
これを解いて
x=9 となります。
よって、「黒ネコ以外のネコがいて、かつ、イヌはいない人」は9人となります。

