その他コンテンツ
中学生のコース
神奈川統一模試 練習問題 解答・解説
数学
-
問1a<0ということは右下がりのグラフとなるので、xが最小のときyが最大となり、xが最大のときyが最小となる。あとは(-3,1)と(1,-9)を通る直線の式を求めればよい。
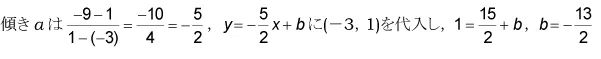
-
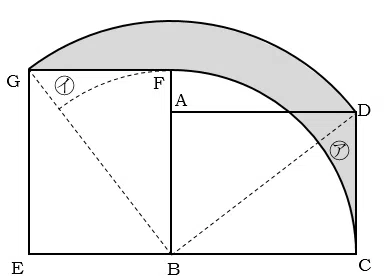
問2対角線BG,BDをひく。これにより影の部分の面積は、おうぎ形GBD+△BCD-△GFB-おうぎ形FBCとなるので、
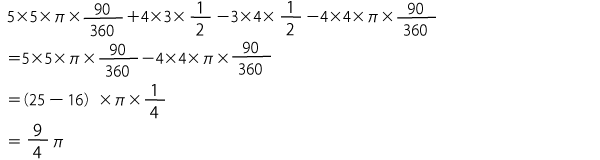
(別解) 右の図で?の部分を?の部分に移すことができる。
すると求める面積は,半径5㎝中心角90°のおうぎ形から半径4㎝中心角90°のおうぎ形を引けば求めることができるので、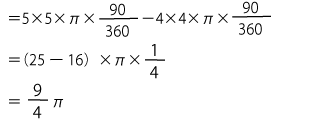
-
問3平均値が3.6冊なので、40人の合計の冊数は3.6×40=144冊
ヒストグラムの38人の読んだ本の合計は134冊なので、AさんとBさんの読んだ本の合計は10冊となる。
また、中央値が3.5冊になるので、20人目は3冊、21人目は4冊とならなければならず、38人のヒストグラムを見ると1~3冊に20人となっているので、AさんもBさんも4冊以上であることがわかる。さらにAさんの読んだ本の冊数はBさんの読んだ本の冊数より多いので、Aさんが6冊、Bさんが4冊とわかる。
特色検査
-
(ⅰ)※このことから、少なくとも縦・横のいっぽうが3の倍数となっている正方形や長方形は必ずトロミノで敷き詰めることができる。
トロミノは正方形を3つつないだ形なので、敷き詰めることができるのは正方形の個数が3の倍数となる盤面に限られる。n×nのうち最小の3の倍数は3×3=9であり、右の図のように敷き詰めることができる。
よって、n=3。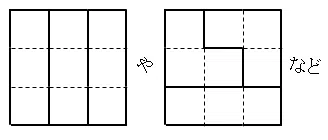
-
(ⅱ)23×23は8×8=64であり3の倍数でないので敷き詰めることはできない。
?あ:できない
8×8の盤面に収まる「3の倍数を1辺とする正方形」は6×6で、(ⅰ)よりこの部分は必ず敷き詰められる。
残る部分は2×6と6×2と2×2の3つの部分に分けられる。
2×6と6×2の2つの部分は6が3の倍数なので必ず敷き詰められる。
2×2の部分は、右図のように影のついた部分を埋めることができないがここが欠ける1マスとなるので、23×23のうち右下の角が1マス分かけている盤面を敷き詰めることはできる。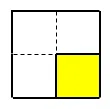
?い:できる26×26についても同様に考え、64×64の盤面に収まる「3の倍数を1辺とする正方形」は63×63で、(ⅰ)よりこの部分は必ず敷き詰められる。
残る部分は1×63と63×1と1×1の3つの部分に分けられる。
1×63と63×1の2つの部分は63が3の倍数なので必ず敷き詰められる。
1×1の部分はトロミノを1つも置くことができずそのまま余るがここが欠ける1マスなので問題ない。
?う:できる
模試・講座・説明会



